eGC - Matlab Tool for computing
the extended Granger Causality
Granger causality (GC) is a very popular tool for assessing the presence of directional interactions between two time series of a multivariate data set [1] . The present toolbox implements the estimation of the GC measure, both in its traditional formulation [1] and in an extended formulation (the so-called extended GC (eGC)) which we recently proposed to account for the possibly confounding effects of zero-lag correlations among the observed time series [2].
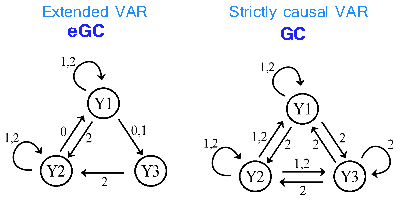
The traditional formulation of the GC is based on a strictly causal vector autoregressive (VAR) model which describes
only the time-lagged effects between the time series, but does not
account for the instantaneous (i.e. not-lagged) effects. As a
consequence of this incomplete description, the presence of significant
instantaneous effects may lead the standard VAR models to provide wrong
interpretations about causality [3]. The measure of extended GC
proposed in our recent study [2] overcomes the limitations of GC by
properly accounting for zero-lag effects in the linear regression
schemes implemented by the VAR model. In [2] we also present a
procedure for the practical estimation of eGC which addresses the
problem of assigning instantaneous effects to the regression models.
This procedure employs a two-step approach based on first estimating
the existence of zero-lag correlations between two processes, and then
orienting them along one of the two possible causal directions using
pairwise measures of non-Gaussianity [4].
|
|
References:
[1] Bressler S L and Seth A K 2011 Wiener-Granger Causality: A well established methodology. Neuroimage 58 323-9.
[2] L Schiatti, G Nollo, G Rossato, L Faes, 'Extended Granger causality: a new tool to identify the structure of physiological networks', Phys. Meas. 2015; 36:827-843.
[3] Hyvarinen A, Zhang K, Shimizu S and Hoyer P O 2010 Estimation of a Structural Vector Autoregression Model Using Non-Gaussianity. J. Machine Learning Res. 11 1709-31.
[4] Hyvarinen A and Smith S M 2013 Pairwise Likelihood Ratios for Estimation of Non-Gaussian Structural Equation Models. J. Machine Learning Res. 14 111-52.
DOWNLOAD:
Zip file with all scripts and functions: eGC.zip
DISCLAIMER OF WARRANTIES AND LIMITATION OF LIABILITY The code is supplied as is and all use is at your own risk. The authors disclaim all warranties of any kind, either express or implied, as to the softwares, including, but not limited to, implied warranties of fitness for a particular purpose, merchantability or non - infringement of proprietary rights. Neither this agreement nor any documentation furnished under it is intended to express or imply any warranty that the operation of the software will be error - free. Under no circumstances shall the authors of the softwares provided here be liable to any user for direct, indirect, incidental, consequential, special, or exemplary damages, arising from the software, or user' s use or misuse of the softwares. Such limitation of liability shall apply whether the damages arise from the use or misuse of the data provided or errors of the software.
The toolbox contains functions for computing the GC (gcMVAR.m; auxiliary function: LinReg.m, LinReg_Ftest.m, SetLag.m)
and the eGC (egcMVAR.m; this function finds the directions of
instantaneous effects exploiting the pairwise measures of
non-Gaussianity proposed by Hyvarinen and Smith [4]: functions
pwling.m, mentappr.m).
For
testing the tool, we provide the script test_simulation.m that
implements the simulation described in [2]; the scripts makes use of
the functions CElin_analytic.m and CElin_analytic_0.m (to find exact
theoretical values of GC and eGC for linear systmes with known
coefficients), diag_coeff_rev.m (to move from strictly causal to
extended VAR representation), and InstModelfilter.m and MVARfilter.m
(to generate realizations of the simulation).