msID - Matlab Tool for multiscale Information Decomposition
Understanding how multiple inputs may combine to create the output of a given target is a fundamental challenge in many fields, in particular in neuroscience. Shannon's Information Theory is the most suitable frame to cope with this problem: the interaction information decomposition (IID) indeed measures the balance between redundant and synergetic interaction within the classical multivariate entropy-based approach; the recent extension of Shannon's Information Theory leading to the Partial Information Decomposition (PID) led to provide specific measures for the information that several variables convey individually (unique information), redundantly (shared information) or only jointly (synergistic information) about the output.
The contribution of our work [1] is the proposal of an analytical frame where both IID and PID can be exactly evaluated across multiple timescales, for multivariate Gaussian processes,
on the basis of simple vector autoregressive (VAR) identification. In
doing this, our work opens the way for both the theoretical analysis
and the practical implementation of information modification in
processes that exhibit multiscale dynamical structures.
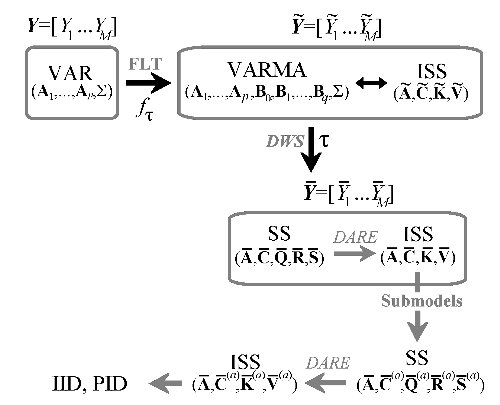
The Matlab toolbox presented here allows to compute analytically the parameters of a VAR model represented at multiple time scales, and to obtain from these parameters exact multiscale values for the information measures composing the IID and PID involving two drivers and a target inside a multivariate stochastic process. This is done exploiting the theory of state-space models, elaborating recent results provided in [2] and [3]. The reader is referred to the main paper [1] for details about the computation.
|
|
References:
[1] L Faes, D Marinazzo, S Stramaglia, 'Multiscale information decomposition: exact computation for multivariate Gaussian processes', Entropy, special issue on Multivariate entropy measures and their applications, 2017, 19(8), 408. DOI: 10.3390/e19080408.
[2] Barnett, L.; Seth, A.K. Granger causality for state-space models. Phys. Rev. E 2015, 91, 040101.
[3] Solo, V. State-space analysis of Granger-Geweke causality measures with application to fMRI. Neural
Computation 2016, 28, 914–949.
DOWNLOAD:
Zip file with all scripts and functions: msID.zip
The code is provided free of charge. It is neither exhaustively tested nor particularly well documented. The authors accept no liability for its use. Use, modification and redistribution of the code is allowed in any way users see fit. Authors ask only that authorship is acknowledged and ref. [1] is cited upon utilization of the code in integral or partial form.
DISCLAIMER OF WARRANTIES AND LIMITATION OF LIABILITY The code is supplied as is and all use is at your own risk. The authors disclaim all warranties of any kind, either express or implied, as to the softwares, including, but not limited to, implied warranties of fitness for a particular purpose, merchantability or non - infringement of proprietary rights. Neither this agreement nor any documentation furnished under it is intended to express or imply any warranty that the operation of the software will be error - free. Under no circumstances shall the authors of the softwares provided here be liable to any user for direct, indirect, incidental, consequential, special, or exemplary damages, arising from the software, or user' s use or misuse of the softwares. Such limitation of liability shall apply whether the damages arise from the use or misuse of the data provided or errors of the software.
To get started, we recommend that you run and work through the two demonstration scripts.
Demonstration scripts
--------------------
- test_simulation - Computes multiscale IID and PID measures for a simulated Gaussian 4-variate process, according to Sect. 4 in [1]
- test_application - Performs VAR identification and computes multiscale IID and PID measures for an example of the public data used as application in [1]. (loads the data in example_data.mat)
Main computational functions
---------------------------
- iss_PCOV - Calculate partial variances from the innovations form state space parameters
- iss_ds - Calculate innovations form state space parameters for a downsampled state space model
- ss2iss - Compute innovations form parameters for a general state space model by solution of a discrete algebraic Riccati equation (DARE)
- varma2iss - Compute parameters of an innovations form state space model from the parameters of the equivalent vector ARMA model
- mos_idMVAR - Model Order Selection for identification of strictly causal VAR model
- idMVAR - identification of strictly causal VAR model
NOTE: the iss_ds and ss2iss functions are taken from the State-Space
Granger Causality Matlab Toolbox -
http://users.sussex.ac.uk/~lionelb/downloads/ssgc.zip