eMVAR - Extended Multivariate Autoregressive Modelling Toolbox
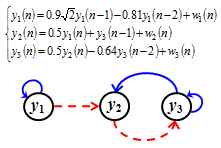 Multivariate
(MV) time series analysis is nowadays extensively used to investigate
the concept of connectivity in dynamical systems through approaches
which are ubiquitous, for instance, in the study of physiological time
series. The analysis of connectivity is not only important to detect
coupling, i.e., the presence or absence of interactions, between the
considered processes, buSt also to identify causality, i.e., the
presence of driver-response relationships. Quantitative assessment of
connectivity is commonly performed representing the considered MV time
series as a realization of a linear MV autoregressive (MVAR) process,
and deriving measures of coupling and causality from the frequency
domain representation of the process. The most popular of these
measures are the Coherence (Coh) (1), the Partial Coherence (PCoh)
(2,3), the Directed Coherence (DC) (4), the Partial Directed Coherence
(PDC) (5) and related measures (directed transfer function (DTF) (6,7),
generalized PDC (gPDC) (8). Coh and PCoh are symmetric measures, which
can be decomposed into factors eliciting directionality, these factors
being exactly the DC and the PDC. More specifically, these four
measures describe in the frequency domain the time domain concepts of
coupling (Coh), direct coupling (PCoh), causality (DC), and direct
causality (PDC). Therefore, PCoh and PDC measure direct connectivity
between two processes, while Coh and DC account for both direct and
indirect connections.
Multivariate
(MV) time series analysis is nowadays extensively used to investigate
the concept of connectivity in dynamical systems through approaches
which are ubiquitous, for instance, in the study of physiological time
series. The analysis of connectivity is not only important to detect
coupling, i.e., the presence or absence of interactions, between the
considered processes, buSt also to identify causality, i.e., the
presence of driver-response relationships. Quantitative assessment of
connectivity is commonly performed representing the considered MV time
series as a realization of a linear MV autoregressive (MVAR) process,
and deriving measures of coupling and causality from the frequency
domain representation of the process. The most popular of these
measures are the Coherence (Coh) (1), the Partial Coherence (PCoh)
(2,3), the Directed Coherence (DC) (4), the Partial Directed Coherence
(PDC) (5) and related measures (directed transfer function (DTF) (6,7),
generalized PDC (gPDC) (8). Coh and PCoh are symmetric measures, which
can be decomposed into factors eliciting directionality, these factors
being exactly the DC and the PDC. More specifically, these four
measures describe in the frequency domain the time domain concepts of
coupling (Coh), direct coupling (PCoh), causality (DC), and direct
causality (PDC). Therefore, PCoh and PDC measure direct connectivity
between two processes, while Coh and DC account for both direct and
indirect connections.
The parametric model traditionally used to compute Coh, PCoh, DC and
PDC is a strictly causal MVAR model, whereby only lagged effects are
modeled, while instantaneous (i.e., not lagged) effects among the time
series are not described by any model coefficients. Nevertheless,
neglecting instantaneous effects may lead to detection of misleading
connectivity patterns. We have recently shown that causality measures
may be adversely affected by the exclusion of instantaneous effects in
the model representation9. To overcome this limitation, we have
proposed the utilization of an extended MVAR model which combines both
instantaneous and lagged effects in order to achieve a full description
of the correlation structure of the observed set of time series (9-11).
The extended model allows computation of the same connectivity measures
than the traditional strictly causal one: while Coh and PCoh are
identical, DC and PDC may be evaluated either including or excluding
instantaneous effects in the computation of the causality measure; in
the first case the resulting measures, lDC and lPDC, consider only
lagged effects, in a similar way to DC and PDC but resolving the
problems related to model mis-specification; in the second case the
resulting measures, eDC and ePDC, are novel extended measures of
causality and direct causality in which instantaneous causality is
accounted for in combination with the traditionally studied lagged
causality (12). Note that, in the absence of instantaneous effects,
both lagged and extended measures of causality and causality are
equivalent to the to traditional measures, because the extended
model reduces to the classic strictly causal model.
Update Jun 2013: the eMVAR framework is now published in:
L Faes, S Erla, A Porta, G Nollo: 'A framework for assessing frequency domain causality in physiological time series with instantaneous effects', Philosophical Transactions A, special issue on “Assessing Causality in Brain Dynamics and Cardiovascular Control”; 2013;371:20110618 (21 pages).
The eMVAR Toolbox
The eMVAR Matlab Toolbox performs both traditional MVAR analysis and extended MVAR analysis, deriving the corresponding frequency domain measures of connectivity from the time domain model coefficients. The toolbox provides also several algorithms for the identification of the two models from time series data, and is completed with algorithms for model validation and for the estimation of frequency-domain significance thresholds. It contains a set of functions realizing model identification and validation and frequency domain analysis, as well as a set of scripts illustrating the utilization of the various functions. The code conforms to methods and notation as described in Faes and Nollo (12), which is available from this link.
DOWNLOAD:
Zip file with all scripts and functions: eMVAR.zip
Note: the “functions” and “external” directories need to be added to the MATLAB path for proper working.DISCLAIMER OF WARRANTIES AND LIMITATION OF LIABILITY The code is supplied as is and all use is at your own risk. The authors disclaim all warranties of any kind, either express or implied, as to the softwares, including, but not limited to, implied warranties of fitness for a particular purpose, merchantability or non - infringement of proprietary rights. Neither this agreement nor any documentation furnished under it is intended to express or imply any warranty that the operation of the software will be error - free. Under no circumstances shall the authors of the softwares provided here be liable to any user for direct, indirect, incidental, consequential, special, or exemplary damages, arising from the software, or user' s use or misuse of the softwares. Such limitation of liability shall apply whether the damages arise from the use or misuse of the data provided or errors of the software.
DESCRIPTION OF THE TOOLBOX
Functions:
- fdMVAR.m : performs frequency domain connectivity analysis from the parameters of a strictly causal MVAR model; returns causality and coupling measures (i.e., DC, DTF, PDC, gPDC, Coh, PCoh), as well as spectral and transfer function matrices (1).
- fdMVAR0.m : performs frequency domain connectivity analysis from the parameters of an extended MVAR model (12); returns frequency domain spectral functions, as well as frequency domain extended and lagged measures of causality and coupling (eDC, lDC, ePDC, lPDC, Coh, PCoh).
- idMVAR.m : identification of strictly causal MVAR model: estimates model coefficients, innovations and innovation covariance from a given time series and a given model order. The default identification algorithm is the standard least squares method (12), but several other algorithms may be recalled (13).
- idMVAR0prior.m : identification of extended MVAR model through the approach using prior information to estimate the instantaneous model: estimates strictly causal and extended model coefficients, innovations and innovation covariance.
- idMVAR0ng.m : identification of extended MVAR model through the approach using non-gaussianity of the innovations to estimate the instantaneous model: estimates strictly causal and extended model coefficients, innovations and innovation covariance.
- mos_idMVAR.m : model order selection for strictly causal MVAR model, using Akaike Information Criterion14 or Minimum description Length criterion (15).
- test_whiteness.m : test for whiteness of strictly causal model residuals; it is the multivariate Ljung-Box portmanteau test (16)
- test_independence.m : test for independence of strictly causal model residuals; may be Spearman rho or Kendall tau test.
- test_gaussianity.m : test for gaussianity of strictly causal residuals; it is the Jarque-Bera test for non-normality (16).
- surrVFT.m : generation of FT surrogates for testing the significance of the coherence (17).
- surrVCFTf.m : generation of causal FT surrogates in which full causality from one series to another is destroyed; they can be used for testing the significance of the DC18. This implementation works for a strictly causal MVAR model.
- surrVCFTd.m : generation of causal FT surrogates in which only direct causality from one series to another is destroyed; they can be used for testing the significance of the PDC18. This implementation works for a strictly causal MVAR model.
- surrVCFTf0.m : generation of causal FT surrogates in which full causality from one series to another is destroyed; they can be used for testing the significance of eDC and lDC18. This implementation works for an extended MVAR model.
- surrVCFTd0.m : generation of causal FT surrogates in which only direct causality from one series to another is destroyed; they can be used for testing the significance of the ePDC and lPDC (18). This implementation works for an extended MVAR model.
- InstModelfilter.m : realizes strictly causal residuals of assigned dimensionality, given either their instantaneous covariance or their dependence on extended residuals (i.e., given instantaneous effects and instantaneous covariance of extended residuals); in the second case, non-gaussianity may be allowed for the extended residuals.
- MVARfilter.m : yields a single realization of a strictly causal MVAR process of assigned dimensionality and length, given strictly causal coefficients and residuals.
- choldiag.m : performs diagonal Cholesky decomposition; useful to derive extended input covariance and mixing matrix (related to instantaneous effects matrix) from the strictly causal input covariance.
- diag_coeff_rev.m : moves from extended MVAR representation to strictly causal MVAR representation (useful in Section 1 only when coeffs are given in the extended representation)
- simuMVARcoeff.m : generates the theoretical coefficients of some illustrative MVAR processes (9,12,19).
Scripts:
- example1.m : runs the theoretical example 1 in Faes and Nollo (12), generating Figs 2,3,4, i.e., spectral functions and decompositions for an illustrative strictly causal MVAR process.
- example1_realization.m : performs a full realization of the theoretical example 1 in Faes and Nollo (12) (and of any other theoretical MVAR process in simuMVARcoeff.m). The script computes the theoretical strictly causal model describing the given process as well as the theoretical frequency domain functions, generates a finite length realization of the process, estimates the strictly causal model and spectral functions from the realization, performs tests on the residuals, as well as full significance testing through surrogates.
- example2.m : runs the theoretical example 2 in Faes and Nollo (12), generating Figs 6,7,8, i.e., spectral, coupling and causality functions for an illustrative extended MVAR process.
- example2_realization_prior.m : performs a full realization of the theoretical example 2 in Faes and Nollo (12) (and of any other theoretical MVAR process in simuMVARcoeff.m). The script computes the theoretical extended model describing the given process as well as the theoretical frequency domain functions, generates a finite length realization of the process, estimates the extended model and spectral functions from the realization, performs tests on the residuals, as well as full significance testing through surrogates. Identification is based on the method using prior information to estimate the instantaneous model.
- example2_realization_ng.m : performs a full realization of the theoretical example 2 in Faes and Nollo12 (and of any other theoretical MVAR process in simuMVARcoeff.m). The script computes the theoretical extended model describing the given process as well as the theoretical frequency domain functions, generates a finite length realization of the process, estimates the extended model and spectral functions from the realization, performs tests on the residuals, as well as full significance testing through surrogates. Identification is based on the method using non-gaussianity of the innovations to estimate the instantaneous model.
External functions:
The toolbox makes use of a set of external functions taken or modified from existing MATLAB toolboxes:
- the BioSig Toolbox (http://biosig.sourceforge.net/), with two functions used for providing various methods for strictly causal MVAR estimation (mvar.m, covm.m);
- the FastICA toolbox (http://research.ics.tkk.fi/ica/fastica), with five functions used to perform Independent Component Analysis in the identification of the instantaneous model based on non-gaussianity of the innovations (fastica.m, remmean.m, pcamat.m, whiten.m, fpica.m);
- the LiNGAM Toolbox (http://www.cs.helsinki.fi/group/neuroinf/lingam), with seven functions used to integrate the identification of the extended MVAR model based on non-gaussianity of the innovations (permnozeribrutal.m, permnozerihungarian.m, permslowertriagbrutal.m, hungarian.m, iperm.m, sltprune.m, slttestperm.m).
References:
-
(1) Kay SM. Modern spectral estimation. Theory & application. New Jersey: Prentice Hall, Englewood Cliffs, 1988.
-
(2) Yacoub.K. Relationship between multiple and partial coherence functions. IEEE Trans Inf Theory 1970; 16(6):668-672.
-
(3) Eichler M, Dahlhaus R, Sandkuhler J. Partial correlation analysis for the identification of synaptic connections. Biol Cybern 2003; 89(4):289-302.
-
(4) Baccala LA, Sameshima K, Ballester G, Valle AC, Timo-Iaria C. Studying the interaction between brain structures via directed coherence and Granger causality. Appl Signal Process 1998; 5:40-48.
-
(5) Baccala LA, Sameshima K. Partial directed coherence: a new concept in neural structure determination. Biol Cybern 2001; 84(6):463-474.
-
(6) Kaminski MJ, Blinowska KJ. A new method of the description of the information flow in the brain structures. Biol Cybern 1991; 65(3):203-210.
-
(7) Kaminski M, Ding M, Truccolo WA, Bressler SL. Evaluating causal relations in neural systems: granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 2001; 85(2):145-157.
-
(8) Baccala L, Sameshima K, Takahashi DY. Generalized partial directed coherence.Proceedings of the 2007 15th International Conference on Digital Signal Processing. Cardiff, UK: 2007.
-
(9) Faes L, Nollo G. Extended causal modelling to assess Partial Directed Coherence in multiple time series with significant instantaneous interactions. Biol Cybern 2010; 103(5):387-400.
-
(10) Erla S, Faes L, Tranquillini E, Orrico D, Nollo G. Multivariate autoregressive model with instantaneous effects to improve brain connectivity estimation. Int J Bioelectromag 2009; 11(2):74-79.
-
(11) Faes L, Nollo G. Assessing frequency domain causality in cardiovascular time series with instantaneous interactions. Methods Inf Med 2010; 49(5):453-457.
-
(12) Faes L, Nollo G. Multivariate frequency domain analysis of causal interactions in physiological time series. In: Laskovski AN, editor. Biomedical Engineering, Trends in Electronics, Communications and Software. Rijeka, Croatia: InTech, 2011: 403-428.
-
(13) Schlogl A. A comparison of multivariate autoregressive estimators. Sign Proc 2006; 86:2426-2429.
-
(14) Akaike H. A new look at the statistical model identification. IEEE Trans Autom Contr 1974; 19:716-723.
-
(15) Rissanen J. An universal prior for the integers and estimation by minimum description length. Ann Stat 1983; 11:417-431.
-
(16) Lutkepohl H. Introduction to multiple time series analysis. Berlin Heidelberg New York: Springer, 1993.
-
(17) Faes L, Pinna GD, Porta A, Maestri R, Nollo G. Surrogate data analysis for assessing the significance of the coherence function. IEEE Trans Biomed Eng 2004; 51(7):1156-1166.
-
(18) Faes L, Porta A, Nollo G. Testing Frequency Domain Causality in Multivariate Time Series. IEEE Trans Biomed Eng 2010; 57(8):1897-1906.
-
(19) Faes L, Erla S, Tranquillini E, Orrico D, Nollo G. An identifiable model to assess frequency-domain granger causality in the presence of significant instantaneous interactions. Conf Proc IEEE Eng Med Biol Soc 2010; 1:1699-1702.